The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics.
Imagine a circle with its center at point O, and a radius drawn from the center to a point on the circle, creating an arc. The angle θ (in radians) is the angle formed when you have an arc whose length is equal to the radius of the circle.
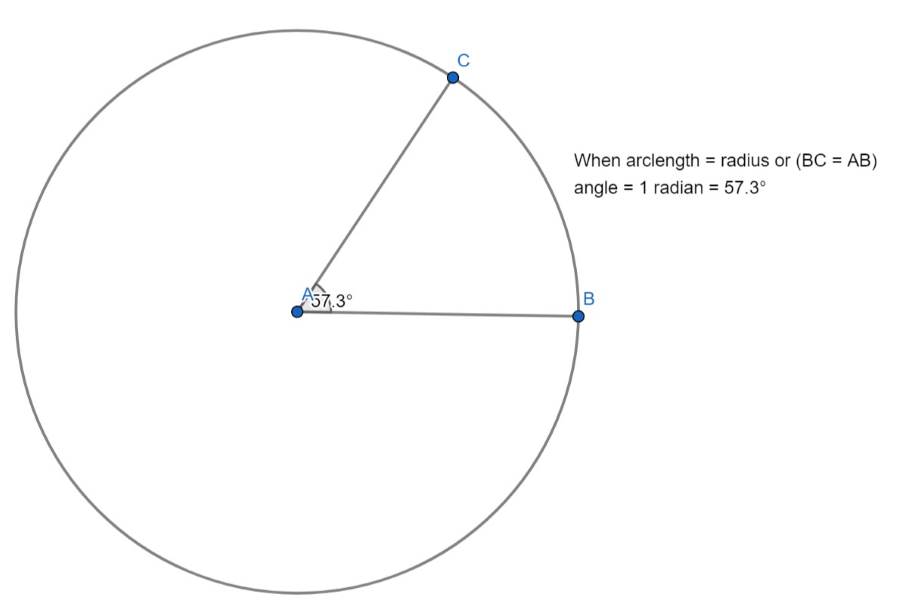
- If the length of the arc is equal to the radius (r), then θ is 1 radian.
- If the arc's length is 2 times the radius (2r), then θ is 2 radians.
- And so on, if the arc's length is n times the radius (nr), then θ is n radians.
In degrees, 1 radian is approximately 57.3 degrees. So, a full circle, 360 degrees, is equivalent to 2π radians, because the circumference of a circle is 2π times its radius.
Use the angle unit calculator to convert radian
The relationship between radians and π (pi)
The relationship between radians and π (pi) stems from the definition of a radian, which is based on the ratio between the length of an arc and the radius of a circle.
In a circle, the circumference (C) is equal to 2π times the radius (r):
C=2πr
Now, if we consider an arc whose length is equal to the radius of the circle (r), the corresponding angle formed at the center of the circle is defined as 1 radian. Therefore, the circumference of the entire circle (C) corresponds to 2π radians.
So, 1 radian is equal to 1/(2π) of the circumference of the circle.
This relationship is essential because it allows us to express angles in terms of radians and vice versa, enabling seamless conversion between angular measures in radians and degrees.