Law of Cosines & Law of Sines

The Law of Cosines

The Law of Cosines is a trigonometric formula used to find the length of a side or measure of an angle in a triangle when two sides and the included angle are known, or when all three sides are known.

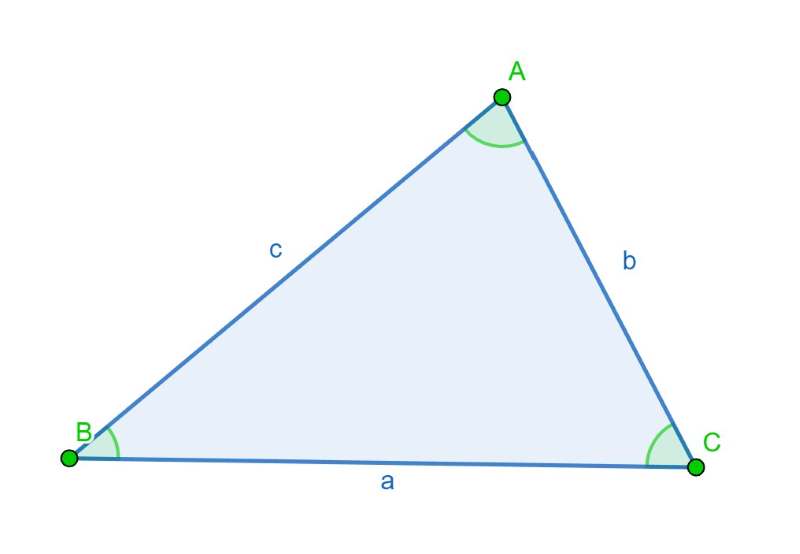
For a triangle with sides of lengths a, b, and c, and angles opposite those sides denoted as A, B, and C respectively, the Law of Cosines states:

$c^2=a^2+b^2-2ab\cos \mathrm{(C)}$

or

$b^2=a^2+c^2-2ab\cos \mathrm{(B)}$

or

$a^2=b^2+c^2-2ab\cos \mathrm{(A)}$

This law is particularly useful when you know the lengths of two sides of a triangle and the measure of the angle between them and you want to find the length of the third side, or when you know the lengths of all three sides and you want to find the measure of one of the angles. (Calculate angles from side length)

The Law of Sines

The Law of Sines is a trigonometric formula used to relate the angles of a triangle to the lengths of its sides. It states that in any triangle, the ratio of the length of a side to the sine of its opposite angle is constant.

For a triangle with sides of lengths a, b, and c, and angles opposite those sides denoted as A, B, and C respectively, the Law of Sines can be written as:

$\frac{a}{\sin \mathrm{(A)}}=\frac{b}{\sin \mathrm{(B)}}=\frac{c}{\sin \mathrm{(C)}}$

This law is useful in various triangle problems, especially when you have information about the angles or sides and need to find missing information. It can also be applied when you have two angles and one side of a triangle and need to find the remaining side lengths.