弧度,以符號 rad 表示,是國際單位制 (SI) 中的角度單位,也是許多數學領域中廣泛使用的角度測量標準。
設想一個圓,其圓心位於 O 點,經過圓心到圓上一點的繪製半徑,便可形成一條圓弧。 角度θ(以弧度為單位)是當圓弧長度等於圓的半徑時所形成的角度。
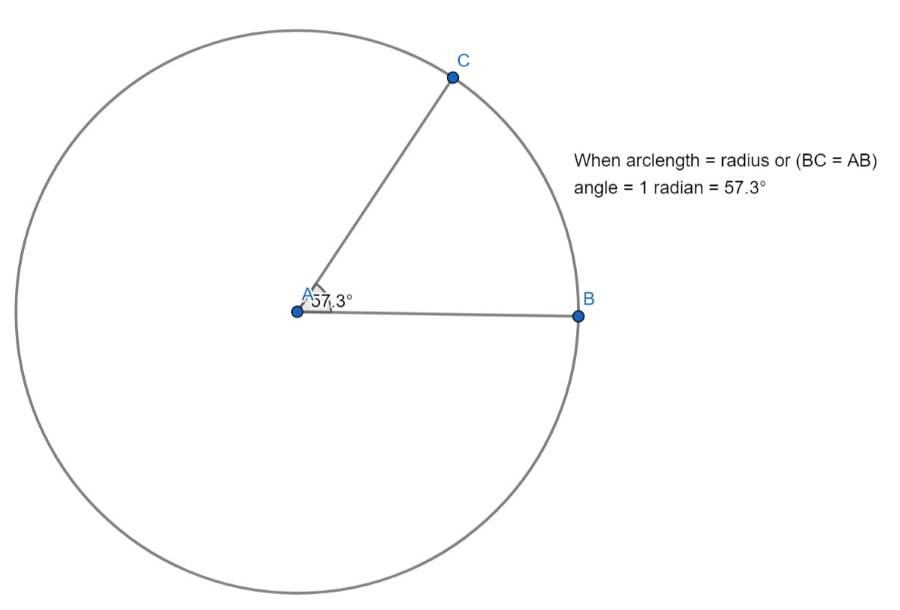
- 若圓弧長度等於半徑 (r),則 θ 為 1 弧度。
- 若弧長是半徑 (2r) 的 2 倍,則 θ 是 2 弧度。
- 依此類推,若弧長是半徑 (nr) 的 n 倍,則 θ 是 n 弧度。
以度為單位時,1 弧度約 57.3 度。 因此,一個完整的圓,360 度,相當於 2π 弧度,因為圓的周長是 2π 乘以其半徑。
弧度與π的關係
弧度與π (pi) 的關係源自於弧度的定義,即弧度是基於圓弧長度與圓半徑之間的比率。
在圓中,週長 (C) 等於 2π 乘以半徑 (r):
C = 2πr
現在,如果我們考慮一條長度等於圓半徑 (r) 的弧,則在圓心處形成的相應角度定義為 1 弧度。 因此,整個圓 (C) 的周長對應於 2π 弧度。
因此,1 弧度等於圓的周長的 1/(2π)。
這種關係至關重要,因為它允許我們以弧度表示角度,反之亦然,從而實現以弧度和度為單位的角度測量之間的無縫轉換。