弧度,以符号 rad 表示,是国际单位制 (SI) 中的角度单位,也是许多数学领域中广泛使用的角度测量标准。
设想一个圆,其圆心位于 O 点,通过圆心到圆上一点的绘制半径,便可形成一条圆弧。角度θ(以弧度为单位)是当圆弧长度等于圆的半径时形成的角度。
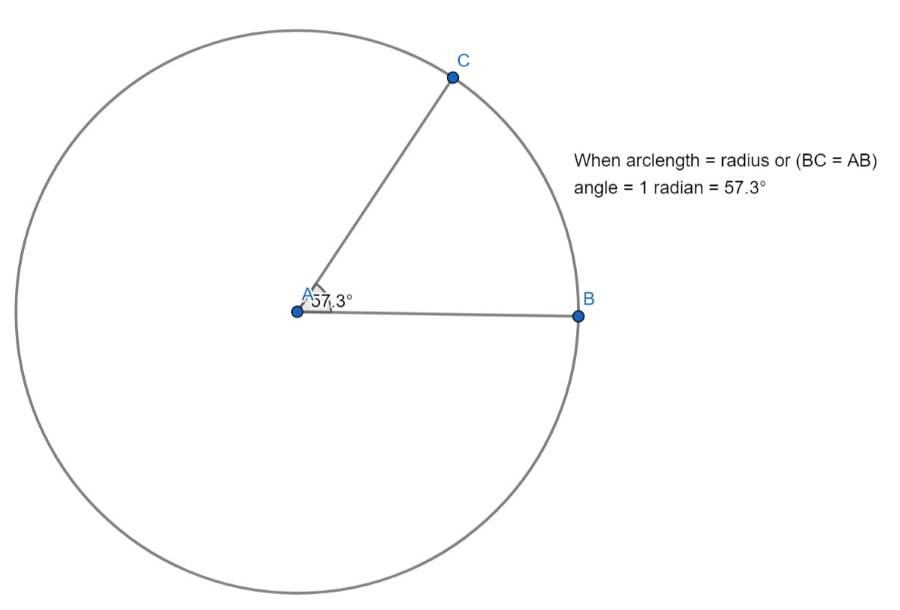
- 若圆弧长度等于半径 (r),则 θ 为 1 弧度。
- 若弧长是半径 (2r) 的 2 倍,则 θ 是 2 弧度。
- 依此类推,若弧长是半径 (nr) 的 n 倍,则 θ 是 n 弧度。
以度为单位时,1 弧度约为 57.3 度。因此,一个完整的圆,360 度,相当于 2π 弧度,因为圆的周长是 2π 乘以其半径。
弧度与π的关系
弧度与π (pi) 的关系源于弧度的定义,即弧度是基于圆弧长度与圆半径之间的比率。
在圆中,周长 (C) 等于 2π 乘以半径 (r):
C = 2πr
现在,如果我们考虑一条长度等于圆半径 (r) 的弧,则在圆心处形成的相应角度定义为 1 弧度。因此,整个圆 (C) 的周长对应于 2π 弧度。
因此,1 弧度等于圆的周长的 1/(2π)。
这种关系至关重要,因为它允许我们以弧度表示角度,反之亦然,从而实现以弧度和度为单位的角度测量之间的无缝转换。